ACTIVITÉ N°4 – Publicité pour un cornet de glace :
Un vendeur de glace souhaite faire une publicité afin d’augmenter ses ventes l’été prochain. Pour y arriver, il voudrait faire un logo à base d’un cornet de glace en s’inspirant des rosaces. Mais avant de faire cette rosace, il aimerait tout comprendre sur les rotations. Voilà la forme de son cornet de glace [Figure 19] et la rosace finale [Figure 20] :

Partie 1 — Mais comment ça tourne ?
1.1 Le cornet de glace de la figure possède-t-il un axe de symétrie ? Si oui, tracer le sur la figure .
1.2 Dans GEOGEBRA, en cochant « Rotation », un deuxième cornet de glace apparaît. Celui-ci a tourné autour d’un point ! Comment peut-on trouver ce point ? Montre les traces de ta recherche sur la figure :
1.3 Dans GEOGEBRA, en cochant « Axes de symétrie des cornets », on remarque que les deux axes se coupent. Comment appelle-t-on ce point, qu’on désignera par « \boldsymbol{R} » ?
1.4 Dans GEOGEBRA, en cochant « Centre de rotation », le point « \boldsymbol{R} » apparait. Il est alors possible de le déplacer. Changer la position du point « \boldsymbol{R} » d’un cran horizontalement à l’aide du curseur « \boldsymbol{h_{1}} ». Que remarque-t-on ? Quelle condition faut-il pour que « \boldsymbol{R} » soit le point d’intersection des deux axes de symétries ?
1.5 Dans la question 1.4, on a vu que les axes de symétries ne permettent pas toujours de trouver le centre de la rotation. Il existe une méthode beaucoup plus efficace pour le trouver à coup sûr. En effet en choisissant deux points sur la figure de départ et en les reliant à leurs points d’arrivés respectifs, on obtient deux segments. Le centre de la rotation est alors le point d’intersection des deux médiatrices de ces deux segments. Applique cette méthode sur la figure :

Dans GEOGEBRA coche dans l’ordre : « Points des cornets », « Segments entre points de départs et points d’arrivés », « Médiatrices », « Centre de rotation » et « Angle de rotation ». Tu pourras ainsi vérifier ta réponse. En modifiant la valeur de l’angle on voit bien qu’on trouve tout le temps le centre de rotation avec cette méthode.
Partie 2 — De combien de degré(s) ça tourne ?
2.1 Dans GEOGEBRA, remettre l’angle de rotation sur « \boldsymbol{60^{\circ}} » et laisse cochées uniquement les cases « Rotation », « Centre de rotation » et « rapporteur » puis vérifier la valeur de cet angle de rotation à l’aide du rapporteur.
2.2 Combien de rotation(s) faudra-t-il effectuer pour représenter une rosace à 6 cornets avec la valeur de l’angle mesurée ? Dans GEOGEBRA laisse cochée uniquement la case « Centre de rotation ». En déplaçant le curseur « \boldsymbol{n} », tu verras alors la rosace apparaitre.
Partie 3 — Des rosaces en veux-tu en voilà !
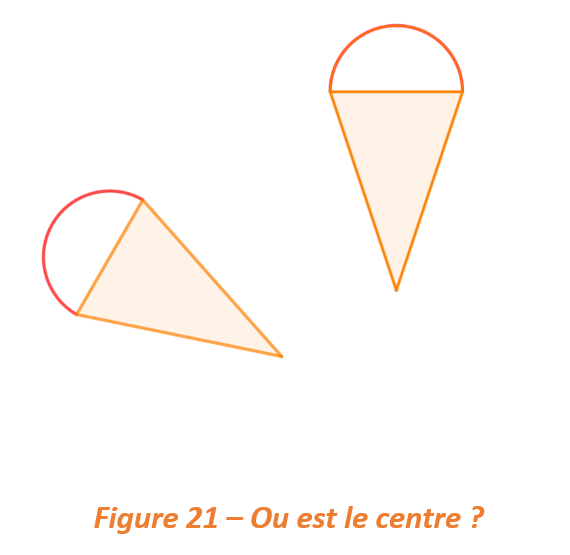
3.1 Sur les deux figures suivantes, trouve le centre de rotation et l’angle de rotation :
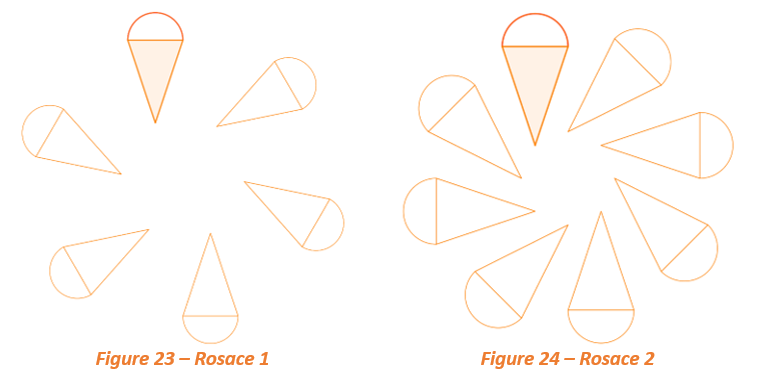
3.2 A ton tour maintenant, compléter la figure suivante pour obtenir une rosace avec 6 cornets par une méthode astucieuse :

Partie 4 — Bilan : Compléter la phrase suivante : Une rotation est une transformation du plan qui consiste à faire tourner un objet autour _______________ et d’un certain _______. Cette transformation conserve les ________, les ________, les ____________ et les ______.
DÉFINITION : Une rotation est une transformation du plan qui consiste à faire tourner un objet (point, ensemble de points, figure…) autour d’un point et d’un certain angle.
EXEMPLE :
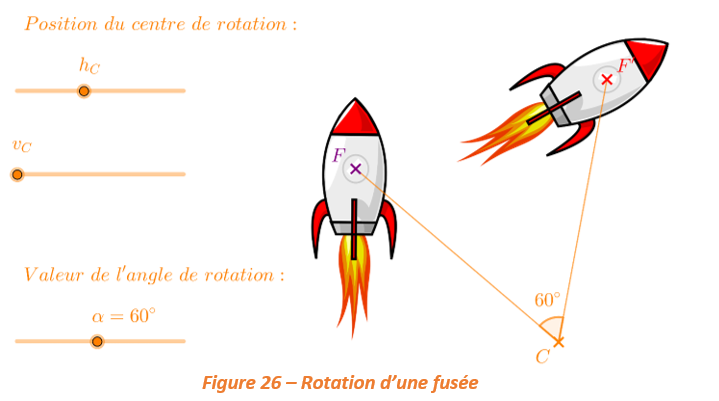
REMARQUE : La fusée de la figure 26 a tourné de \boldsymbol{60^{\circ}} autour du point C .
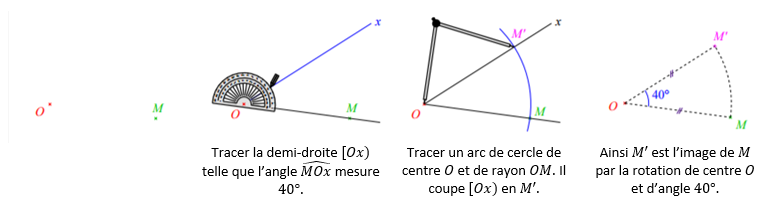
MÉTHODE : ROTATION D’UN POINT AU RAPPORTEUR ET AU COMPAS : Traçons M’ , image du point M par la rotation de centre C et d’angle \boldsymbol{40^{\circ}} autour du point C .
PROPRIÉTÉS : La rotation est une transformation qui conserve, les angles, les distances, les alignements et les aires.
APPLICATION – Construction d’une rosace par rotation :
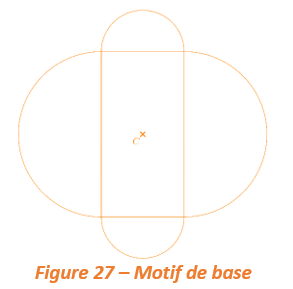
Considérons le motif de base suivant :
Pour construire une rosace, on répétera ce même motif en effectuant plusieurs rotations de même angle de centre C .
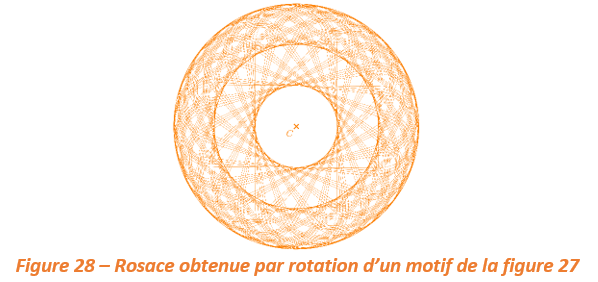
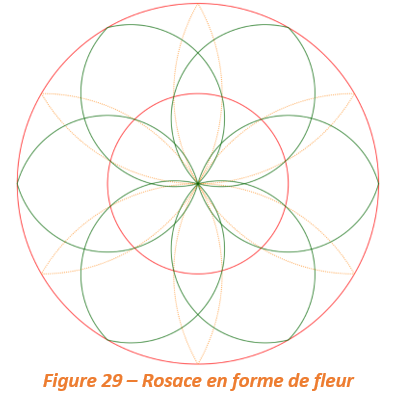
EXERCICE N°6 : Reproduire la rosace en forme de fleur suivante :